
|
PROOF #1 |
||
|
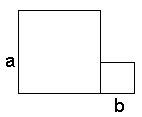
First, we start with two squares with sides a and b, placed side by side with the total area of a2+b2. |
||
|
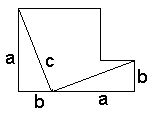
Now we draw two triangles, both with sides a and b and hypotenuse c (the two squares have been removed). Therefore now we have two triangles and a unusual looking shape. |
||
|
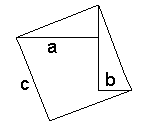
For the last step, we rotate the triangles 90o, each around its top vertex. The right one is rotated clockwise whereas the left triangle is rotated counterclockwise. Obviously the resulting shape is a square with the side c and area c2. |
||
|
PROOF #2 |
||
|
First, we drew a circle with radius c and a the right triangle with sides a and b. In this situation, you may apply any of a few well known facts. For example, in the diagram three points located on the circle form another right triangle with the height of length a. Its hypotenuse is split in the ratio (c+b)/(c-b). So, as in Proof #6, we get a2 = (c+b)(c-b) = c2 - b2. |
||
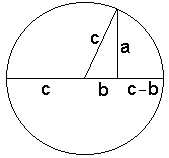
|
ANIMATED PROOF |
||
|
Below is an animated proof of the Pythagorean Theorem. Starting with a right triangle and squares on each side, the middle size square is cut into congruent quadrilaterals (the cuts through the center and parallel to the sides of the biggest square). Then the quadrilaterals are hinged and rotated and shifted to the big square. Finally the smallest square is translated to cover the remaining middle part of the biggest square. A perfect fit! Thus the sum of the squares on the smaller two sides equals the square on the biggest side. |
||

|
Afterward, the small square is translated back and the four quadrilaterals are directly translated back to their original position. The process is repeated forever. |
||